Sie sind hier:
Startseite
> TGG
>
TGG
> Lehrpläne
>
Lehrpläne
> Mathematik
Mathematik
Legende für die Tabellen
- Fett: Schwerpunkt
- Normal: zu bearbeiten
- Kursiv: kann eventuell entfallen
Körper und Figuren
| Thema |
Kommentare |
Neue Medien |
| Systematisierung verschiedener Körper |
|
|
| Systematisierung der Vielecke |
- erste Wenn-Dann-Aussage
- Strecke als Begrenzung
|
erster Einsatz von Euklid möglich |
| Koordinatensystem |
|
|
| Geraden und ihre Lagebeziehungen |
Halbgerade und Strecke |
Euklid |
| Darstellung von Körpern |
Schrägbilder und Körpernetze teilweise schon in der Grundschule |
|
Natürliche Zahlen
| Thema |
Kommentare |
Neue Medien |
| Darstellungsformen |
- Zehnersystem
- Dualsystem
- Bau eines Zahlenstrahls zur weiteren Verwendung im
Unterricht
- Potenzen schon ansprechen
|
|
| Rechnen mit natürlichen Zahlen |
|
|
| Zahlterme |
Sprachliche Umsetzung |
|
Bruchzahlen und Verhältnisse
| Thema |
Kommentare |
Neue Medien |
| Grundvorstellung von Bruchzahlen |
|
|
| Vergleichen und Ordnen |
|
|
Kreis und Winkel
| Thema |
Kommentare |
Neue Medien |
| Kreise |
|
|
| Winkel |
Bau einer Winkelscheibe (Buch Seite 132 Nr. 13) |
|
Dezimalbrüche
| Thema |
Kommentare |
Neue Medien |
| Darstellung |
|
|
| Vergleichen und Runden von DB |
|
|
| Rechnen mit DB |
|
|
Längen, Flächen- und Rauminhalte
| Thema |
Kommentare |
Neue Medien |
| Längen |
Einheiten umrechnen |
|
| Flächeninhalt |
Rechnen mit Brucheinheiten |
|
| Rauminhalt |
|
|
Bruchzahlen II
| Thema |
Kommentare |
Neue Medien |
| Prozente |
|
|
| Mischungsverhältnisse |
|
|
| Maßstab |
Verbindung zu Erdkunde suchen |
|
Daten
| Thema |
Kommentare |
Neue Medien |
| Begriffe |
Buch Seite 285 |
|
| Daten sammeln |
|
Rechnereinsatz (Excel) |
| Daten erstellen |
|
|
| Daten auswerten |
|
|
| Darstellungsformen der Zahlen |
|
|
Rechnen mit Bruchzahlen
| Thema |
Kommentare |
Neue Medien |
Addieren und Subtrahieren von Bruchzahlen
- Kommutativ- und Assoziativgesetz der Addition
|
Gemischte Schreibweise von Bruchzahlen soll lediglich zur Einschätzung von Größen dienen. |
|
Multiplizieren und Dividieren von Bruchzahlen
- Rechengesetze für Multiplikation und Division
|
|
| Berechnen von Termen |
|
|
Zuordnungen – Dreisatz
| Thema |
Kommentare |
Neue Medien |
| Verschiedene Darstellungsformen von Zuordnungen (z. B. Tabelle und Graph) |
|
Excel |
| Proportionale Zuordnungen
(„je mehr – desto mehr“)
|
|
|
| Dreisatz bei proportionalen Zuordnungen |
|
|
| Antiproportionale Zuordnungen („je-mehr-desto-weniger“) |
|
|
| Dreisatz bei antiproportionalen Zuordnungen |
|
|
| Prozentrechnung (Prozentsatz, Prozentwert, Grundwert, prozentuale
Erhöhung, prozentuale Abnahme; Dreisatzanwendung) |
|
|
| Zinsrechnung |
|
|
Symmetrien erkennen und erzeugen
| Thema |
Kommentare |
Neue Medien |
| Parkettierungen |
|
DynaGeo |
| Muster erzeugen und analysieren |
|
|
Kongruenz-
abbildungen
- Schwerpunkt: Achsen- und Punktspiegelung
- Verschiebung
- Drehung
- Doppelspiegelung (Punktspiegelung)
- Geraden
- Scheitelwinkel, Nebenwinkel, Stufenwinkel
- Winkelsummensatz für Dreiecke
- Winkelsummensatz für Vierecke
|
- Verschiebung und Drehung kann zeitsparend am
Rechner durchgeführt werden
- Symmetrien an Dreiecken und Vierecken zur
Vertiefung der Inhalte aus Klasse 5
|
DynaGeo |
Zufall und Prognosen
| Thema |
Kommentare |
Neue Medien |
| einstufige Zufallsexperimente durchführen |
|
|
| Empirisches Gesetz der Großen Zahlen |
|
|
| den Ergebnissen von Zufallsexperimenten Wahrscheinlichkeiten zuordnen
(Schätzen von relativen Häufigkeiten für lange Versuchsreihen) |
|
|
| Additions- und Komplementärregel |
|
|
| Ereignis (sicheres, unmögliches) |
|
|
| Laplace-Wahrscheinlichkeit |
|
|
Rationale Zahlen
| Thema |
Kommentare |
Neue Medien |
| Negative Zahlen – Rationale Zahlen |
|
|
| Erweiterung des Koordinatensystems |
|
|
| Anordnung der rationalen Zahlen |
|
|
Zahlenbereichs-
erweiterung |
|
|
| Addieren und Subtrahieren der rationalen Zahlen, Rechengesetze |
|
|
| Multiplizieren und Dividieren der rationalen Zahlen, Rechengesetze |
|
|
Dreiecke und Vierecke
| Thema |
Kommentare |
Neue Medien |
| Konstruieren von Dreiecken |
- Kongruenz sss / wsw / sws / Ssw
- Problem: sSw
|
DynaGeo (Einstieg) |
| Beweisen – Satz und Kehrsatz |
|
|
| Konstruieren von Vierecken |
|
|
| Besondere Linien und Punkte im Dreieck – Ortslinien |
|
DynaGeo |
| Kreis – Satz des Thales |
Referate |
|
Terme und Gleichungen
| Thema |
Kommentare |
Neue Medien |
| Aufstellen von Termen anwendungsbezogen |
|
Excel |
- Wertgleichheit von Termen /
Rechengesetze (Kommutativ …)
- Termumformungen
|
Division und Subtraktion auf Multiplikation und Addition zurückführen |
Excel |
| Lösen von Gleichungen und Ungleichungen |
Aussageform / Aussage / Grundmenge / Lösungsmenge / Waage-Modell |
|
| Modellieren |
Textaufgaben |
|
Berechnungen an Vielecken und Prismen
| Thema |
Kommentare |
Neue Medien |
| Flächeninhalte |
- Flächeninhalte von Dreiecken
- Vielecke auf Dreiecke und Vierecke zurückführen
|
|
Prisma
- Netz / Schrägbild
- Oberfläche / Volumen
|
- Basteln (Körper / Netze)
- Räumliches Begreifen
- Fächerverbindung Kunst
|
|
Mehrstufige Zufallsexperimente
| Thema |
Kommentare |
Neue Medien |
| Baumdiagramme |
Darstellung / Struktur eines Zufallsexperimentes |
Excel |
| Pfadregeln |
Pfadadditions- und Pfadmultiplikationsregel |
|
Lineare Funktionen
| Thema |
Kommentare |
Neue Medien |
| Funktionsbegriff |
- Eindeutige Zuordnung
- Zuordnungsvorschrift x → f(x)
- Funktionsgleichung y = f(x)
- Funktionsterm f(x)
|
- Einführung GTR
- Menü Graph
- Menü RunMath
|
| Proportionale Funktion |
Tabelle / Graph / Steigung / Änderungsrate (!) |
|
| Lineare Funktionen |
- Verschiebung auf der Y-Achse
- Einführung von Parametern
- y = mx + b (festgelegte Notation!)
|
GTR |
| Nullstellen |
- Achsenschnittpunkte
- Deutung
|
GTR |
| Geraden durch zwei Punkte |
Anwendungsaufgaben |
GTR |
| Modellierung |
- Geraden durch Punktwolken
- Analyse von Diagrammen
|
- Excel Diagramme
- Trendlinien
|
Terme und Gleichungen mit Klammern
| Thema |
Kommentare |
Neue Medien |
| Auflösen einer Klammer |
|
|
| Minuszeichen vor einer Klammer – Subtrahieren einer Klammer |
|
|
| Ausklammern |
|
|
| Auflösen von zwei Klammern in einem Produkt |
|
|
| Binomische Formeln |
|
|
| Faktorisieren einer Summe |
|
|
| Umformen von Formeln |
|
|
| Gleichungen vom Typ T1 · T2 = 0 |
|
GTR: expand, rFctor |
Lineare Gleichungen mit zwei Variablen
| Thema |
Kommentare |
Neue Medien |
| Lineare Gleichungen der Form ax + by = c |
|
Excel |
| LGS: Grafisches Lösungsverfahren |
Alle Fälle |
Auch GTR |
| LGS: Numerische Verfahren |
Additionsverfahren |
GTR, auch CAS |
Quadratwurzeln – Reelle Zahlen
| Thema |
Kommentare |
Neue Medien |
| Quadratwurzeln |
Ein Näherungsverfahren;
z. B. Heron-Verfahren (Blickpunkt) |
|
| Wurzelziehen und Quadrieren |
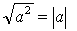 |
|
| Rechenregeln für Quadratwurzeln |
Nachweis nur exemplarisch |
|
| Reelle Zahlen |
Verwendung der Zahlengeraden |
|
| Rechnen mit reellen Zahlen |
|
|
Satz des Pythagoras
| Thema |
Kommentare |
Neue Medien |
| Satz des Pythagoras |
|
|
| Berechnung von Streckenlängen |
|
|
| Umkehrung des Satzes des Pythagoras |
|
|
Parabeln – Quadratische Funktionen und Gleichungen
| Thema |
Kommentare |
Neue Medien |
| Geometrisches Erzeugen von Parabeln |
Ortslinie |
Euklid |
| Quadratfunktion – Eigenschaften der Normalparabel |
|
|
| Quadratische Gleichungen – Grafisches Lösen |
|
GTR: Nullstellen, Schnittpunkte |
| Strecken und Verschieben der Normalparabel |
Parameter-
untersuchungen |
GTR |
| Optimierungsprobleme mit quadratischen Funktionen |
|
GTR |
| Lösen quadratischer Gleichungen |
|
GTR |
| Optimierung mit Quadraten |
Regression |
GTR: LIST |
| Datenpaare grafisch darstellen |
|
GTR |
Modellieren: in jedem Abschnitt
Ähnlichkeit / Trigonometrie
| Thema |
Kommentare |
Neue Medien |
Prozess-
bezogene Kompetenzen |
| Eigenschaften ähnlicher Figuren |
Abgrenzung zum umgangs-
sprachlichen Gebrauch der Ähnlichkeit
|
|
- Modellierung
- Kommunizieren: Abgrenzung der Bedeutung
- Fächerübergriff: Physik: Abstands-Gesetz
|
| Trigonometrie |
- Arcusfunktionen: erst über Graph und x-Calculation, später über Run
- Notationen: arcsin, arccos, arctan
- Vollständigkeits-
überlegungen führen zu Sinussatz und Kosinussatz – diese müssen wenigstens genannt
werden (Hinweis auf Formelsammlung)
|
GTR, Derive |
|
Körper
| Thema |
Kommentare |
Neue Medien |
| Schrägbilder |
|
|
| Körpernetze, Modelle |
|
|
| Formel zur Berechnung des Körpervolumens |
Exemplarische Herleitung an mindestens einem Beispiel |
|
| Schätzungen und Berechnungen von Volumen und Oberfläche |
Zylinder, Pyramide, Kegel, Kugel |
|
| Schätzen und Bewerten an „unregelmäßigen“ Körpern |
Mit Hilfe von ein- bzw. umschreibenden „regelmäßigen“ Körpern |
|
| Berechnungen an einfachen Teilkörpern |
|
|
Statistik und Wahrscheinlichkeitsrechnung
| Thema |
Kommentare |
Neue Medien |
| Datenpaare darstellen, Regression, Prognosen |
Verbinden mit „Wachstum“, „Modellieren“ |
GTR: Punktdiagramme, Regression |
| Zweistufige Zufallsexperimente, Baumdiagramme |
|
|
| Vierfeldertafel, Satz von Bayes |
|
|
Kreis
| Thema |
Kommentare |
Neue Medien |
Prozess-
bezogene Kompetenzen |
| Kreiszahl π |
Mindestens ein Näherungs-
verfahren für π |
Tabellen-
kalkulation – Excel oder GTR |
|
Kreisflächen-
inhalt, Kreisumfang |
Anwendungs-
aufgaben |
|
Modellierung |
Potenzgesetze und Wachstumsprozesse
| Thema |
Kommentare |
Neue Medien |
Prozess-
bezogene Kompetenzen |
| Potenzgesetze |
Kann ganz kurz gehalten werden; es sollte neben den Gesetzen
auf Zehnerpotenzen, Abkürzungen, Rechner-
darstellung eingegangen
werden. |
|
|
Potenz-
funktionen und Exponential-
funktionen
(Grundform) |
Ziel: Grundformen der Graphen;
Streckung, Rückbezug zu quadratischen Funktionen, Verschiebung, Symmetrie, Spiegelung;
Rückbezug zu quadratischen Funktionen;
Parameter-
variationen: es sollten in diesem Zusammenhang
alle mit dem Rechner besprochen werden |
GTR: drei Möglichkeiten der Darstellung von Kurvenscharen |
Modellierung |
| Umkehrfunktionen |
Kann ganz kurz gehalten werden
- Zusammenhang von Potenzen und Wurzeln
- Exponential-
funktionen
- Spiegelung an der 1. Winkel-
halbierenden
- Umformen
- Notation:

|
GTR: CAS, solve Zoom, square |
|
Sinusfunktion
| Thema |
Kommentare |
Neue Medien |
Prozess-
bezogene Kompetenzen |
| Einheitskreis |
Spätestens hier sollte der Einheitskreis
als Übergang zu den Funktionen benutzt werden |
|
|
| Sinusfunktion |
- Parameter-
variationen
- Anwendungs-
aufgaben
|
GTR, Derive |
Modellierung |
Funktionaler Zusammenhang I
| Thema |
Kommentare |
Neue Medien |
Exponentialfunktionen
- Parametervariationen
- Sachtexte auf funktionale Zusammenhänge untersuchen
- Wechsel zwischen Darstellungen
- Wachstums-
zusammenhänge erkennen und klassifizieren
- mit Funktionen Zusammenhänge modellieren, Lösungen bewerten
|
Beschreiben, erläutern, beurteilen
Tabelle, Graph, Term, Gleichung; auch Überlagerung
exponentiell / linear; Einbezug aller Funktionstypen |
GTR
GTR: Listen, Regression
|
Funktionaler Zusammenhang II
| Thema |
Kommentare |
Neue Medien |
| Änderungsraten und Sekantensteigungen in funktionalen Zusammenhängen |
Aus Graph, Term, Tabelle |
GTR |
| Ableitung als lokale Änderungsrate und Tangentensteigung |
beschreiben, interpretieren, berechnen |
GTR |
| Grafischer Zusammenhang zwischen Funktion und Ableitungsfunktion |
|
|
| Ableitungsfunktion für ganzrationale Funktionen bis vierten Grades |
|
GTR |
| Ableitungsregeln |
Summen- und Faktorregel |
|
| Optimierungsprobleme / Sachprobleme |
|
GTR |
Funktions-
untersuchungen unter Verwendung der Ableitung |
|
GTR |
![]() TGG
TGG
![]() Lehrpläne
Lehrpläne
![]() Mathematik
Mathematik